Your homework problem:
You suspect that a gambler’s die is “loaded,” such that its six outcomes are not equally likely. You roll this die 120 times and get the following results:
| Side of Die: | 1 | 2 | 3 | 4 | 5 | 6 |
| Observed Frequency: | 16 | 16 | 10 | 20 | 28 | 30 |
Is this a fair die? In other words, does the obtained pattern of frequencies deviate significantly from what you would expect by chance (i.e., equal probability
You want to know if the obtained frequencies in this study deviate significantly from a proposed model for these frequencies. That’s why this test is called a Goodness of Fit Test — it asks whether your data “fit” a particular theoretical model. In this case, we want to know if the results of throwing this die fits a model of a fair die — one that has six outcomes that are equally probable.
We will use the Chi Square statistic to test the goodness of fit of our model:
where f_o refers to the obtained frequencies in your study and f_e refers to the expected frequencies in your study. k is equal to the number of categories — in our case, k = 6.
The expected frequencies are determined by the theoretical model that you are testing your data (i.e., obtained frequencies) against. In our case, we are testing our data against a model of equal frequency. So, given that we had 120 trials and there are 6 possible categories, we expect to find 20 examples of each outcome (i.e., 20 ones, 20 twos, and so on):
| Side of Die: | 1 | 2 | 3 | 4 | 5 | 6 |
| Observed Frequency: | 16 | 16 | 10 | 20 | 28 | 30 |
| Expected Frequency: | 20 | 20 | 20 | 20 | 20 | 20 |
Computing the Chi Square statistic is simple, but you need to be patient with the number of steps involved:
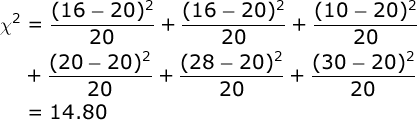It’s a good idea here to use the memory function in your calculator: a) clear your calculator’s memory, b) compute the first segment of this equation and place the result in your memory, and c) compute each other segment of the equation and add each to your memory. When you are done, just recall the sum that is in your calculator’s memory (14.80).
Conduct hypothesis test. In our case, k = 6 so the df for our Χ² test will be 5, and alpha = .05. From your table of critical values for the Χ² test, you will find that if the value of our obtained Χ² is greater than 11.07, we would conclude that the outcomes of this die are not equally probable.
Since 14.80 is greater than 11.07, we would conclude that this is not a fair die — it’s outcomes are not equally probable.